3次元任意形状の解析が可能- 誘電体や磁性体を含む構造物の解析が可能
- モーメント法により高精度・高速解析を同時実現
- 高次基底関数により少ない未知数で高精度・高速解析を同時実現
- 四辺形パッチにより未知数が半減し、高精度・高速解析を同時実現
- Smart ReductionやMLFMMにて大規模解析に最適
WIPL-D高次基底関数モーメント法（境界要素法）の基本動作を動画にてご覧頂けます。 
WIreとPLateでモデルを作成し、境界面の電流分布を求めるモーメント法は(1次元当り)有限要素法の1/7のアンノーン数で同じ精度を実現
WIPL-D モーメント法（境界要素法）とFEM（有限要素法）やFDTD法との差異を動画にてご覧頂けます。 空間を含む解析対象でも高精度・高速解析が可能であることをFEM（有限要素法）やFDTD法との対比で動画にてご覧頂けます。 
RWG等の低次基底関数と比較し大幅に(約1桁)少ない分割数(アンノーン数)で同じ精度を実現
高次基底関数（全領域展開）と低次基底関数（部分領域展開）の差異を動画にてご覧頂けます。 
三角パッチと比較して半分のアンノーン数で同じ精度を実現
四辺形パッチと三角形パッチの差異を動画にてご覧頂けます。 
76.5GHz/半径185mmレンズアンテナ(約94波長)
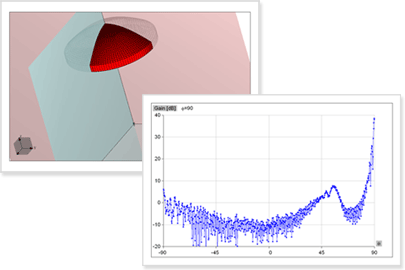
Optimizerによるモデル最適化事例
- アンテナ解析
- ワイヤーアンテナ、ホーン及び開口アンテナ、リフレクタアンテナ、アレイアンテナ、ヘリカルアンテナ、マイクロストリップアンテナ等
- アンテナ配置
- 大きな構造物近傍での放射パターン解析
- 散乱解析
- 航空機、車両など任意形状に対するRCS及び電流分布解析
- EMC
- ラジエーションハザード、カップリング、シールド解析等
- マイクロ波回路及び導波管
- フィルタ、カプラ、共振子等
- 誘電体及び磁性体における電磁界解析
- 人体細胞に対する電磁界解析を含む